|
|
|
1. Úvod.
Po neúspešných pokusoch vysvetliť zákonitosti tepelného žiarenia absolutne čierneho telesa na základe klasickej fyziky, pokúsil sa o vysvetlenie M.Planck. Absolútne čierne teleso si predstavil ako sústavu harmonických oscilátorov, ale na rozdiel od svojich predchodcov vyslovil domnienku, že ich energia sa môže meniť len spojito. Jednoduchú metódu odvodenia zákona, ku ktorému dospel Planck, ukázal neskôr Einstein. Ako je dobre známe, vysvetlenie zákonov o vyžarovaní tepla a fotoelektrických javov viedlo k zrodu kvantovej mechaniky. Preto všetky také pokusy, ktoré umožňujú kvantitatívne overiť tieto javy zaujímajú dôležité miesto vo vyučovaní fyziky. Experimentálny dôkaz Stefanovho-Boltzmannovho zákona, čo je vlastne integrálny tvar Planckovho zákona emisie svetla, je veľmi ťažká úloha, preto na jeho overenie sa možno podujať len na veľmi málo miestach.
Cieľom tejto úlohy je overiť Stefanovho-Boltzmannov zákon spôsobom, ktorý možno realizovať aj v laboratóriách, vybavených jednoduchým zariadením.
Pri odvodení Planckovho zákona sa
vychádza z predstavy, že absolútne čierne teleso sa skladá z atómov,
ktoré sú v rovnovážnom stave so žiarením. Budeme ďalej predpokladať, že
atómy môžu byť v stavoch s energiami W1, W2, ...,Wn,
...,Wm. Počet atómov s energiou Wn určuje
Boltzmannov zákon:
| (1) |
| kde: | N0 je konštanta. |
Pokus dokazuje, že atóm môže samovoľne
prejsť zo stavu s vyššou energiou Wm do stavu s nižšou
energiou Wn, pričom:
| Wm-Wn = h.nmn, | kde nmn je frekvencia vyžiareného kvanta; | |
| h=6,6.10-34 Js je Planckova konštanta. |
Od Planckovho postulátu (energia
elektromagnetického poľa je distribuovaná v kvantách určených vzťahom -
W=hn) sa
dostaneme k Planckovmu vyžarovaciemu zákonu:
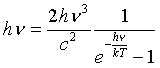 |
(2) |
spôsobom, ktorý je uvedený napríklad v učebnici: A. Štrba, Všeobecná fyzika 3 - Optika, Alfa 1979.
Rozborom tohto zákona dostaneme odpoveď
na všetky otázky týkajúce sa žiarenia absolútne čierneho telesa. Nás
zaujíma teraz celková žiarivosť absolútne čierneho telesa E0.
Hodnota E0 sa nájde integrovaním Planckovho zákona (2) cez
všetky frekvencie
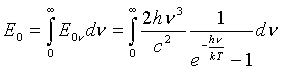 |
(3) |
Po výpočítaní integrálu dostaneme:
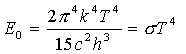 |
(4) |
a to je Stefanov-Boltzmannov zákon, podľa ktorého celková žiarivosť povrchu absolútne čierneho telesa je úmerná štvrtej mocnine jeho absolútnej teploty. Hodnota Stefanovho-Boltzmannovej konštanty s=5,67.10-8Wm-2.K-4.
Ak teleso nie je absolútne čierne, potom
sa rovnica (4) prejde na tvar:
| E0=eAs T4, | (5) | |
| kde: | ||
| A je emisný povrch; | ||
| e je úplná emisná schopnosť daná vzťahom: | ||
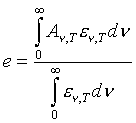 |
(6) | |
| kde: | ||
| An,T je absorpčná schopnosť ; | ||
| en,T emisná schopnosť; | ||
| Integrál v menovateli predstavuje integrálnu emisnú schopnosť absolútne čierneho telesa. |
![]()
2. Fyzikálna podstata
spôsobu overenia Stefanovho-Boltzmannovho zákona.
V našom experimente sa ako emisný zdroj
použije volfrámová žiarovka (0< e< 1). Energia:
| E0 = I2R | (7) |
dodávaná elektrickým zdrojom do obvodu
sa spotrebúva na
vedenie tepla a na vyžarovanie. V stave rovnováhy
platí:
| E0 = I2R = P(T-T0)n + eAs T4-QT04 | (8) | ||
| kde: | |||
| P a Q konštanty; | |||
| n » 1; | |||
| T0 je teplota prostredia (izbová teplota). | |||
Ak teplota prevyšuje 1000oK,
je T4 >> T04 a rovnica (8) sa
zjednoduší na tvar:
| I2R = P(T-T0)n + eAsT4 | (9) |
Pri dostatočne nízkych teplotách (T <
500 K) sú straty tepla žiarením (vo vzťahu 8) zanedbateľné oproti
stratám tepla vedením, teda člen eAsT4-QT04 je
zanedbateľný oproti P(T-T0)n. Straty tepla
vedením možno teda počítať zo vzťahu:
| I2R = P(T-T0)n | (10) |
Pri zobrazení rovnice (9) v log-log
sústave dostaneme nasledujúce výsledky:
|
|
dá sa dokázať, že pri nízkej teplote (po T ~ 500oK) sú rozhodujúcou formou straty tepla vedením (koeficient úmernosti ~ 1). |
|
|
straty tepla vedením extrapolované k vyšším teplotám odčítané od úplného výkonu nám dávajú smerový tangens ~ 4, čo znamená potvrdenie Stefanovho-Boltzmannovho zákona. |
Kritickým bodom experimentu je určenie
teploty vlákna žiarovky. Odpor kovov v závislosti od teploty je určený
ako:
| R = R0[1+a(T-T0)], | (11) | |
| kde: | ||
| R0 je odpor pri izbovej teplote T0, | 2 | |
| a teplotný súčiniteľ elektrického odporu, pre volfram je a = 0,0053 |
Keď R0 poznáme, potom teplota
sa určí ako:
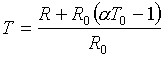 |
(12) |
Na určenie odporu R0 žiarovky možno použiť dva spôsoby. Pri prvom sa pomocou Wheatsonovho mostíka určí priamo odpor, pri druhom sa určuje volt - ampérová charakteristika žiarovky.
Oba spôsoby majú aj výhody aj nevýhody. Pri dobrom odporovom mostíku sa v prvom prípade dá odpor merať s presnosťou na tisíciny ohmu; nevýhodou je, že cez meraný odpor musí prechádzať určitý prúd I a určenie R0/R=f(I) pri extrapolovaní k I=0 nie je presné. U druhého spôsobu je menšia presnosť určenia odporu, ale sa dá aj pri veľmi malých prúdoch cez rezistor presne určiť hodnota R0. Je to umožnené tým, že funkcia R=f(I2R) približne pri izbovej teplote t.j. pri veľmi malom výkone je lineárna. (Odpor vlákna je približne 1/12 odporu pripadajúceho na maximálny výkon).
3. Experimentálne
prevedenie a výsledky.
K experimentu sú k dispozícii dve volfrámové žiarovky rozdielneho výkonu ako zdroje žiarenia. K určeniu hodnoty ich odporu R0 pri izbovej teplote sa použije druhý spôsob, t.j. bude sa snímať veľkosť prúdu cez žiarovku v závislosti od napätia. Odpor R0 sa určí zo smernice priamky preloženej nameranými bodmi U=f(I). Pri známej izbovej teplote T0 sme potom pomocou vzťahu (12) schopní vypočítať teplotu vlákna žiarovky pre každý bod volt-ampérovej charakteristiky.
Pri meraní V-A charakteristiky na určenie odporu R0 je nutné pracovať v oblasti veľmi malých napätí a prúdov, aby sa zaručil minimálny ohrev vlákna (podľa typu aparatúry použijeme buď prúdový zdroj alebo reostat na na jemnú reguláciu a obmedzenie skokového nárastu prúdu pri prepínaní rozsahov napájacieho zdroja). Výkon žiarovky pri týchto hodnotách je o niekoľko rádov menší ako je nominálna hodnota. Napätie je vhodné merať elektrónkovým voltmetrom, ktorý má veľmi vysoký vnútorný odpor.
Po určení odporu R0 a zadaní izbovej teploty T0 pokračujeme v meraní volt-ampérovéj charakteristiky žiarovky v celom pracovnom rozsahu napätí a prúdov (až po nominálnu hodnotu napätia, uvedenú na žiarovke - samozrejme už bez ochranného reostatu).
Aby sa mohla uvážiť strata vedením tepla
najprv sa znázorní úplný výkon do grafu v závislosti od T-T0,
teda musíme určiť konštanty P a n vo vzťahu (10) s pomocou
zlogaritmovaného vzťahu (10):
| ln(I2R) = ln P+ n*ln (T-T0)n | (13) |
Koeficient n teda dostaneme ako smernicu k1 preloženej priamky y = k1x + q1 a konštantu P vypočítame z q1=lnP.
Teraz sme už schopní určiť energiu
žiarenia. Straty tepla vedením extrapolované k vyšším teplotám ((Tł 500K) odčítame od úplného
výkonu a dostaneme straty
výkonu pri emisii:
| Pe= I2R - P(T-T0)n = eAsT4, | (14) |
ktoré treba zobraziť do grafu závislosti
od T. Po zobrazení závislosti strát tepla žiarením od teploty T (13) v
log-log sústave smernica preloženej priamky určuje hľadaný exponent.
V súvislosti s vyhodnotením musíme upozorniť na:
- Určité ťažkosti sa môžu vyskytnúť pri určení bodu, v ktorom sa oddeľujú od seba krivá a rovná časť grafu t.j. problém od ktorej teplote (T-T0) začínajú byť podstatné straty žiarením. Zo skúsenosti vieme, že pri dostatočnom počte meraní pri (T-T0)~200-700oC sa dajú dobre oddeliť obe časti grafu, nakoľko straty tepla pri nízkej teplote (T-T0<=300K) sú úmerné prvej mocnine rozdielu teplôt. V prípade nami používaných volfrámových žiaroviek straty tepla vedením možno optimálne extrapolovať smernicou m» 0,97, čo zaručuje dobré východisko pre reálny koncový výsledok.
- Pri vyšších teplotách (T>=1000K), kde má žiarenie rozhodujúcu úlohu, nemožno celkom zanedbať straty tepla vedením. Na ilustráciu sú v tabuľke 1. zahrnuté straty vedením tepla (i) v percentách vzťahujúce sa na úplný výkon pre rôzne teploty. Pri zanedbaní strát vedením tepla značne klesne strmosť krivky emisných strát, v prípade 220 V žiarovky o 30%.
| Tab.1. | Straty výkonu spôsobené vedením tepla (i ) v závislosti od celkového výkonu žiarovky pri rôznych teplotách. | ||||
| Žiarovka |
|
||||
| T=1500K | T=2300K | T=2500K | |||
| 220 V | 22,5 | 10,6 | - | ||
Uvedené skutočnosti môžu pomôcť objasniť prípadné odchýlky hľadaného exponentu m od želanej hodnoty 4. Nakoľko sme od celkového výkonu najprv podľa vzťahu (14) odpočítali straty tepla vedením a na vyhodnocovanie závislosti emisného výkonu od teploty používame údaje s vysokými teplotami (1500K < T < 2500K) možno pri najvyššich teplotách (podľa tabuľky 1 v okolí T~ 2500K) obdržať exponent m<4. Ako optimálna oblasť údajov pre m~4 nemusí byť teda oblasť údajov s maximálnymi teplotami. Ak teda výsledkom Vášho merania bude napríklad smernica m~3,86 môžete to pokladať ako dodatočný dôkaz platnosti Stefanovho-Boltzmannovho zákona, teda potvrdenie, že emisné straty sú úmerné štvrtej mocnine teploty.
Pracovné úlohy:
- Odmerajte závislosť prúdu cez žiarovku od napätia zo zdroja. Vyhodnotenie vykonajte podľa programu z počítača.
|
|
|