Každá častica pohybujúca sa hmotným prostredím postupne stráca pozdĺž dráhy letu svoju počiatočnú kinetickú energiu. Strata energie závisí od druhu a kinematických parametrov častice, jej interakcie, od vlastností prostredia a dĺžky jej interakčnej dráhy v ňom.

Preto definujeme straty energie na jednotkovej dĺžke dráhy –dE/dx, ktoré nazývame špecifické straty energie. V niektorej literatúre ich uvádzajú pod názvom lineárna brzdná schopnosť látky (1, 2). U ťažkých elektricky nabitých častíc sú tieto straty spôsobené hlavne

ich elektromagnetickou interakciou s obalovými elektrónmi atómov /molekúl, kryštálov/prostredia, čo vedie k excitácii a ionizácii týchto atómov. Preto ich často nazývame aj spoločným názvom ionizačné straty. V dôsledku týchto strát sa okamžitá rýchlosť častice pozdĺž jej dráhy letu postupne neustále zmenšuje, čo vedie k ich funkčnej závislosti od okamžitej rýchlosti častice.

m - pokojová hmotnosť elektrónu
(epsilon) - permitivita vákua
B – tzv. koeficient /faktor/ brzdenia. V niektorej literatúre sa pod ním rozumie súčin Z.B (3). 

Je to bezrozmerná veličina, ktorá závisí nielen od vlastností prostredia, ale aj od rýchlosti pohybu častice.

Použijúc zákony klasickej elektrodynamiky pre ťažké nerelativistické častice ho určil v r. 1913 N.Bohr. Vychádzal pritom z tzv. minimálneho a maximálneho účinku /váhovanej strednej vzdialenosti/ interakcie častice s elektrónmi prostredia.

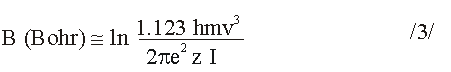
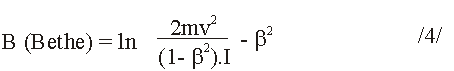
kde ß = v/c je relativistická rýchlosť pohybu častice a c rýchlosť svetla vo vákuu. Priebeh ionizačných strát od Lorentzovho faktora gama je v semilogaritmickej škále ukázaný plnou čiarou na obr. 1.
 
 

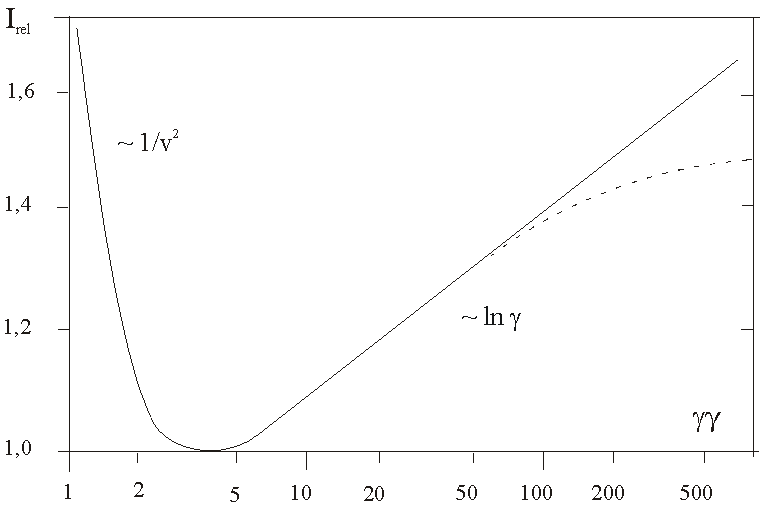Obr. 1. Typická závislosť relatívnych špecifických strát energie v plynoch pri normálnych podmienkach od Lorentzovho faktora gama (na obr. je pre gama použité grécke písmeno) Irel = (dE/dx)/(dE/dx)min.; gama = E/E0 = m/m0 = 1/(1-ß 2 )0.5  E0; m0 – pokojová energia a hmotnosť častice E; m – celková relativistická energia a hmotnosť častice

Pri malých rýchlostiach energetické straty s rastom energie častice prudko klesajú / približne 1/v², vzťah / 2 // , prechádzajú minimom a pre gama> 4 logaritmicky rastú. Túto oblasť, ktorej zodpovedá lineárne rastúci úsek uvedenej krivky, spôsobenej členom ß vo vzťahu /4/, nazývame oblasť logaritmického rastu energetických strát /približne ~ ln(gama)/. 

Podľa Betheho modelu interakcie relativistický rast energetických strát s rastom energie častíc neustále pokračuje. Experimenty však ukázali, že tento rast je pomalší /ako logaritmický/, až sa nakoniec zastaví. Pri veľmi vysokých energiách už energetické straty nezávisia od energie častíc a krivka ionizačných strát vychádza na tzv. Fermiho plató (4). Preto v r. 1933 vypracoval F. Bloch komplexnejší model interakcie ťažkých častíc na základe kvantovej relativistickej elektrodynamiky. V nej pre faktor B vychádza zložitá logaritmická gamma funkcia komplexnej premennej, z ktorej ako limitné prípady vyplývajú vzťahy /3/ a /4/ (1, 3). V zjednodušení možno výsledky Blocha napísať v tvare: 

Dosadením tohto vzťahu do rovnice /2/ dostaneme Bethe-Blochovu formulu pre výpočet ionizačných strát (3).

Funkciu delta (E) súvisiacu s energiou častice a vlastnosťami prostredia nazývame faktor /efekt/ polarizácie alebo hustoty prostredia. Má za následok zmenšenie energetických strát častíc s veľmi vysokými rýchlosťami /gama > 50/.Súvisí s deformáciou culombovského poľa interagujúcej častice, ktorá vedie k polarizácii atómov prostredia /posuv elektrónov oproti atómovým jadrám/, t.j. k vzniku dipólov z neutrálnych atómov /molekúl/, čo sa javí ako „odtienenie“ časti náboja interagujúcej častice. Tento efekt je tým výraznejší čím je hustota elektrónov /a teda i atómov / prostredia väčšia /preto aj efekt hustoty/. Jav polarizácie vedie k tomu , že logaritmický rast špecifických strát sa postupne s rastom energie častíc zastaví a tieto vychádzajú na Fermiho plató. Vplyv tohto efektu je ukázaný čiarkovanou krivkou na obr.1. Priebeh tejto krivky je málo závislý od prostredia a druhu v ňom interagujúcich častíc. Minimum energetických strát sa nachádza v oblasti gama = /3-4/. Napr. pre protóny je 3 GeV, pre alfa častice približne 12 GeV. Relativistický rast ionizačných strát /minimum-Fermiho plató/ je u pevných látok rádovo percentá, u plynov pri normálnom tlaku rádovo 10%. Popisom a meraním efektu polarizácie sa zaoberalo viacero významných fyzikov. Medzi inými aj E.Fermi, L.D.Landav, E.M.Lifšic a E.M.Sternheimer (3). 

Všetky tri uvedené modely interakcie platia za predpokladu, že hmotnosť interagujúcej častice M a jej okamžitá energia E spĺňajú podmienky M ›› m a E ›› E(ion), kde E(ion) je maximálna ionizačná energia obalových elektrónov atómov prostredia. Tieto nerovnosti sú exaktným vyjadrením predpokladu, že interagujúca častica pozdĺž svojej dráhy nemení príliš smer pohybu a nezachytáva obalové elektróny atómov prostredia, čím nemení veľkosť svojho elektrického náboja.

Podotkneme, že relativistické častice strácajú energiu aj inými spôsobmi. Ako príklad uvedieme prechodové, Čerenkovovo a brzdné žiarenie, tiež jadrové reakcie. Energetické straty spôsobené týmito interakciami sa riadia inými zákonitosťami a pre ťažké, nerelativistické častice sú malé v porovnaní s ionizačnými stratami. 

Podľa spomenutých troch modelov interakcie možno z ich zovšeobecneného vzťahu /2/ urobiť nasledovný záver. Pri prechode ťažkej elektricky nabitej častice látkovým prostredím sú jej špecifické ionizačné straty energie:

i /. Úmerné kvadrátu náboja častice a nezávisia od jej hmotnosti 
ii /. Rastú s atómovým číslom prostredia / zhruba lineárne /
iii/.Pri nerelativistických rýchlostiach vzrastajú s poklesom ich rýchlosti približne podľa vzťahu: dE/dx = const./v²
 
 

ŠSE

Zadanie

Táto úloha má tzv. „teoretickú" (výpočtovú) a experimentálnu časť. V teoretickej časti budeme uvažovať, že pre ťažké nerelativistické častice, funkčná závislosť f(v) vo vzťahu /1/ spĺňa jeden z nasledujúcich predpokladov:

C. Špecifické straty nie sú funkciou rýchlosti častice v, t.j., že pozdĺž celej svojej dráhy na jednotke dĺžky stráca častica rovnaké (konštantné) množstvo energie.
 

G. Straty so zmenšovaním rýchlosti rastú , avšak podľa vzťahu:

Vezmeme tiež do úvahy nasledujúce z experimentov známe výsledky:

1. Súvis medzi doletom R alfa častíc a ich počiatočnou energiou E₀ sa riadi tzv. Geigerovým empirickým pravidlom (5): 

2. Medzi dráhou x alfa častice ktorú táto preletí v hmotnom prostredí a jej zostatkovou /teda nepohltenou / energiou E/x/ platí tzv. Geigerovo poloempirické pravidlo (2): 

Teoretické úlohy:

1. Ukážte výpočtom, že alfa častice emitované prírodnými rádioizotopmi možno považovať za nerelativistické častice. Vyvoďte z toho dôsledok, ktorý využijete v nasledujúcej úlohe.
2. Predpoklady C, B, G preveďte z diferenciálnych na integrálne tvary vo forme E(x) = f(x) a x = f(E). Ktorý z týchto predpokladov vyhovuje poloempirickému vzťahu /7/? Dokážte, že ak je správny predpoklad: C- potom E(x) = f(x) musí byť priamka, B- potom E²(x) = f(x) musí byť priamka a pre G - funkcia E^3/2(x) = f(x) musí byť priamka.
3. Pre všetky tri predpoklady nájdite funkciu R = f(E). Ktorý z predpokladov vyhovuje vzťahu /6/? 
4. Pre uvedené predpoklady vypočítajte polohu ťažiska ionizácie častíc ako funkciu ich doletu R. Ktorý z nich vyhovuje empirickému vzťahu /8/?
5. Pre všetky predpoklady vypočítajte hodnotu dE/dx na prvom centimetri dráhy alfa častice s počiatočnou energiou E₀ = 5.48 MeV /R = 40 mm/ vo vzduchu. Za „prvý“ centimeter považujte úsek /1.4 – 11.4/ mm od ich zdroja. Ktorý z predpokladov vedie k skutočnosti opísanej tzv. Braggovou krivkou?

6. Pomocou polovodičového Si(Li) detektora zmerajte funkčnú závislosť E(x) = f(x) vo vzduchu pre alfa častice emitované izotopom ²⁴¹Am, ktorých počiatočná kinetická energia je približne 5.48 MeV.
7. Výsledky merania graficky znázornite funkčnými závislosťami E(x) = f(x), E²(x) = f(x) a E^3/2(x) = f(x), ktoré zodpovedajú predpokladom C, B, G. Podľa výsledkov úlohy č.2 musí byť pre správny predpoklad táto závislosť lineárna. Rozhodnite ktorý to je!
8. Špecifické straty energie na „prvom“ centimetri dráhy alfa častice vychádzajú pre každý z predpokladov ináč. Určite ich z vašich meraní a z porovnania výsledkov v úlohe č. 5 rozhodnite ktorý z predpokladov je správny. 
9. Z Vášho experimentu nájdite ťažisko ionizácie a z jeho polohy zistite, ktorý z predpokladov je správny.
10. Určite dolet R alfa častíc z experimentu.
11. Určite experimentálnu chybu vašich výsledkov v úlohách č.8, 9 a 10.
12. Prediskutujte a odôvodnite neštandartný výsledok vašich výpočtov a meraní.

Postup a návod k riešeniu úloh.

1. Uvedomte si, že počiatočná kinetická energia alfa častíc leží v intervale E₀ = (3-10) MeV. Stačí vyjadriť Lorentzov faktor gama resp. relativistickú rýchlosť beta pre najväčšiu z nich (napr. E₀ = 10 MeV). Z výsledku vyplýva, že medzi ich okamžitou rýchlosťou v a kinetickou energiou E možno s dostatočnou presnosťou použiť vzťah:

2. Predpokladajme obecnejší vzťah:

• Pre x = 0 musí byť E(x) = E₀. Odtiaľ:

• Pre x = R musí byť E(x) = 0. Odtiaľ vypočítame konštantu D.

3.  Hľadanú funkciu dostaneme z rovnice /12/ pri požiadavke splnenia okrajovej podmienky b. v predchádzajúcej úlohe.
4. Polohu ťažiska ionizácie dostaneme zo vzťahu /12/, v ktorom určíme konštantu D z podmienky b. a skutočnosti, že pre x = x₀ musí byť E(x₀) = E₀/2.
5. Zo vzťahov E(x) = f(x) zistených v úlohe č.2 vypočítame hodnoty E(x) pre x = 1.4mm a x = 11.4 mm. Ich rozdiel udáva stratu energie alfa častice na jej „prvom“ centimetri dráhy.
6. Ako zdroj nerelativistických ťažkých častíc použite alfa častice vyžarované izotopom 241 Am s počiatočnou kinetickou energiou E₀ = 5.48 MeV. Registrujte ich polovodičovým detektorom Si(Li) o ktorom predpokladáte,že medzi v ňom pohltenou (teda zbytkovou ) energiou alfa častice E a amplitúdou signálu A platí vzťah:

7. Z nameraných polôh maxím (kanálov) v diferenciálnych spektrách zostavte tabuľku A = f(x), A² = f(x) a A^3/2= f(x) pre x = (1.4; 6.4; 11.4; 16.4; 21.4; 26.4; 31.4; 36.4) mm a výsledky znázornite v troch grafoch. Ak máte možnosť, dáta v nich fitujte pomocou polynomickej funkcie (napr. druhého stupňa). Z tvaru kriviek rozhodnite , ktorý z predpokladov C, B, G je správny, t.j. najlepšie opisuje vami namerané hodnoty. 

8.  Z polohy maxima v amplitúdovom spektre pre prvé meranie určite kalibračnú konštantu K vo vzťahu /13/ pre váš spektrometer. Uvážte, že poloha tohto maxima zodpovedá minimálnej vzdialenosti zdroj-detektor, ktorá je 1.4 mm a preto nezodpovedá presne energii E₀ = 5.48 MeV, ale menšej. Jej hodnotu určite výpočtom z úlohy č. 2, alebo extrapoláciou správnej krivky z úlohy č.7. Z kalibrácie a polohy maxím vypočítajte energie prislúchajúce vzdialenostiam 1.4 a 11.4 mm. Ich rozdiel bude hľadaná stredná strata energie v „prvom“ centimetri dráhy alfa častice vo vzduchu. Porovnajte ju z výsledkami v úlohe č. 5 a urobte príslušný záver.

9. Extrapolujte správnu krivvku z úlohy č.7 pre x = 0 mm a najdite jej amplitúdu v tomto bode. Poloha polovice z nej zodpovedá ťažisku ionizácie. Najdite ju buď interpoláciou medzi susednými experimentálnymi bodmi, alebo z analytického vyjadrenia príslušnej krivky.

10. Extrapolujte krivky z úlohy č.7 k hodnote A = 0.

11. Berte do úvahy iba chybu, ktorá vznikne z nepresnosti určenia polôh maxím v nameraných dif. spektrách. Tá zodpovedá hodnote 1 kanál. 

12. 12. Z vášho experimentu, ako i z výpočtov jednoznačne vyplýva správnosť predpokladu G. Ako je to možné? Snáď sa traja mohykáni fyziky (z ktorých dvaja sú nositeľmi Nobelovej ceny) mýlili? Nie! Ich výsledky, u nás uvedené predpokladom B, platia pre prípad, kedy dE/dx ‹‹ E, t.j. častica stratí pri interakcii nepodstatnú časť svojej okamžitej energie. To bude vtedy ak: 

•  Ide o jednorázovú interakciu s absorbátorom (terčom), ktorý má jednoatómovú vrstvu. Vtedy však veličina dE/dx ako strata energie na jednotke dĺžky absorbátora zvyčajne nemá fyzikálny zmysel (opodstatnenie). Výnimkou môže byť napr. veľmi zriedený plyn. V reálnom plyne ,napr. vo vzduchu pri atmosferickom tlaku, vytvorí alfa častica počiatočnej energie 5.48 MeV na jednom centimetri v priemere približne 5.48.10⁶/4.30 =45 000 iónových párov a preto model o jednorázovej interakcii nepripadá do úvahy.

• Ide o relativistické (resp. kvázirelativistické) častice, t.j. častice majúce podstatne väčšiu energiu ako energia, ktorú stratí každá z nich pri interakcii s jednotkovou dĺžkou absorbátora. Potom sa však metódou absorbcie nedá určiť ich dolet v prostredí.

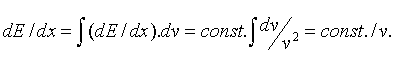/14/

Vidíme, že ustrednením formúl Bohra, Betheho a Blocha dostávame predpoklad Geigera. Z tohto hľadiska vzťah dE/dx = const./v² nepredstavuje straty energie v jednotkovej hrúbke absorbátora, ale iba hodnotu dE/ (jedna interakcia) prepočítanú na jednotkovú dĺžku absorbátora.
 
 

ŠSE

Záver

 

Ťažká, nerelativistická, elektricky nabitá častica preletom cez hmotné prostredie na dĺžke svojej dráhy ležiacej v intervale (x₁, x₂) stráca energiu: 
 
 

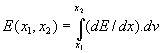kde hodnota: 
 

predstavuje stredné špecifické straty okamžitých energetických strát prislúchajúcich jednorázovej interakcii prepočítanej na jednotkovú dĺžku dráhy interakcie častice (zodpovedajúce vzťahom 2; 3; 4; 5) t.j. počítať dvojný integrál týchto vzťahov:
 
 

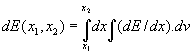Poznámky autora:

1. H.Geiger nikdy nezaviedol pre špecifické straty energie predpoklad G. Tento predpoklad sme nazvali Geigerov v dôsledku toho, že z neho vyplývajúce poloempirické vzťahy /6/ a /7/ nesú jeho meno.
2. Ďakujem p. L. Derzsimu a p. B. Žilkovi, poslucháčom KJF FMFI UK a mojej dcére za iniciatívu a pomoc pri prevedení môjho rukopisu a časti neusporiadaných poznámok k tejto úlohe do počítačovej formy.

1. J.Šeda a kol.: Dozimetrie ionizujíciho záření. Praha, SNTL 1983
2. Š.Šáró: Detekcia a spektrometria žiarenia alfa a beta. Bratislava, Alfa 1983
3. Ju.A.Budagov i drugie: Ionizacionnye izmerenija v fizike vysokych energij. Moskva, Energoatomizdat 1988
4. K.N.Muchin: Experimentaľnaja jadernaja fizika. T.1. Moskva, Atomizdat 1974
5. M.Florek a kol.: Fyzikálne praktikum IV. (Atómová fyzika a detekcia ionizujúceho žiarenia) Bratislava, vyd. UK 1988.